Recursively Enumerable languages
Recursively Enumerable languages: If any Turing Machine can be designed to accept all string of the given language, then the language is called recursively enumerable language.
Recursively enumerable languages are the formal languages that can be decide-able, ( fully or partially). According to the Chomsky hierarchy of formal languages, we can see the recursively enumerable languages as type 0 languages. some examples of recursively enumerable languages are;
- Recursive languages
- Regular languages
- Context-sensitive languages
- Context-free languages and many more.
Recursively enumerable language is recursively enumerable if it can be accepted by the Turing machine (Read More). This is the main reason why recursively enumerable languages are also called Turing recognizable languages. Please note that the Turing machine is a very strong machine as compared to the finite state automata or pushdown automata and is more powerful than many other machines.
Properties of Recursively enumerable languages
- Union
- Intersection
- Complement
Union of RE languages
Let’s revise union of sets;
Set 1={a, b, c}
Set 2={b, c, d}
Set 1 Union Set 2 = {a, b, c, d}
Now let’s understand the same concept in Turing Machine;
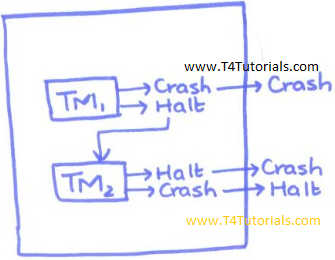
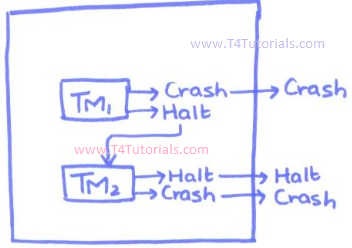
Suppose a system has 2 Turing Machines, TM1, and TM2.
- If TM1 halts then all the system halts.
- If TM1 crash then system checks that TM2 is ready to halt or not? If TM2 halts then system halts because this is union and the union means that
- If TM1 halts then system halts
- If TM1 does not halt, and TM2 halts then system halts
- If TM1 and TM2 or TMn halts then system halts
The intersection of RE languages
Let’s revise the intersection of sets;
Set 1={a, b, c}
Set 2={b, c, d}
Set 1 Intersection Set 2 = {b, c}
Now let’s understand the same concept in Turing Machine;
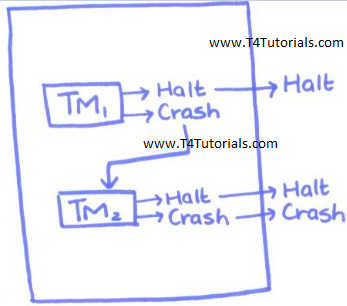
Suppose a system has 2 Turing Machines, TM1, and TM2.
- If TM1 crash then all the system crash.
- If TM1 halts then system checks that TM2 is ready to halt or not? After this, If TM2 halts then system halts because this is intersection and the intersection means that
- If TM1 crash then system crash
- If TM1 halts then check TM2 or TMn, and if TM2 is also halted, the system halts.
- If TM1 and TM2 or TMn crash then the system crash
The complement of RE languages
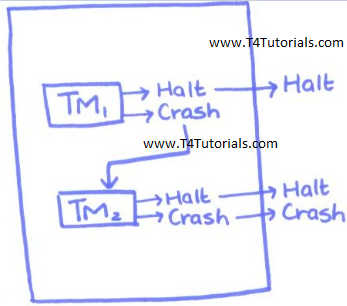
Suppose a system has 2 Turing Machines, TM1, and TM2.
- If TM1 crash then all the system crash.
- If TM1 halts then system check TM2 or TMn. If TM1 halts and TM2 also halts then system crash.
- If TM1 halts then system check TM2 or TMn. If TM1 halts and TM2 crash then system halts.